Note de la rédaction: Le 8 octobre 2013, Peter Higgs et François Englert ont reçu le prix Nobel de physique pour leurs travaux sur le boson de Higgs. Ci-dessous, notre chroniqueur scientifique Brian Greene explique les fondements scientifiques de la découverte.
De cette histoire
[×] FERMER
Le détecteur ATLAS, l'une des deux expériences visant à repérer le boson de Higgs, insaisissable, lors de l'accumulation de particules dans le Grand collisionneur de hadrons du CERN, pèse jusqu'à cent 747 jets et abrite plus de 1 800 km de câbles. (Claudia Marcelloni / CERN) 
Le solénoïde compact de muon situé au niveau du grand collisionneur de hadrons capte les particules. (Michael Hoch / CERN)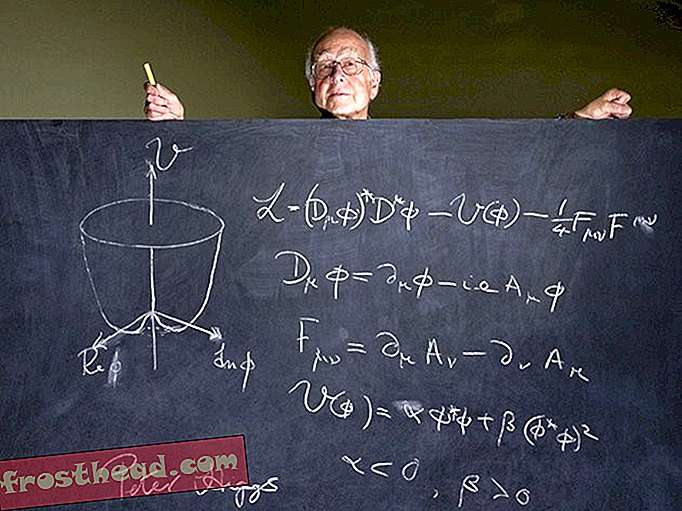 
Retour à la planche à dessin: Le physicien Peter Higgs dessine sa célèbre équation décrivant la source de la masse d'une particule. Il faudrait un demi-siècle pour prouver la vérité. (Stuart Wallace / Splash News / Newscom) 
L’équipe travaille avec le détecteur ATLAS, l’une des deux expériences permettant de repérer l’insaisissable boson de Higgs dans des smashup de particules. (Claudia Marcelloni / CERN) 
Avant l'installation, des parties du détecteur CMS vivaient dans une salle de nettoyage au CERN. (Maximilien Brice, Michael Hoch et Joseph Gobin / CERN) 
L'aimant dans le détecteur CMS produit un champ magnétique 100 000 fois plus puissant que celui de la Terre. (Gobin / CERN) 
Un gros plan du détecteur CMS - une des deux expériences visant à détecter les signatures du boson de Higgs. (Gobin / CERN) 
Bien que le boson de Higgs apparaisse trop brièvement pour être détecté directement, les physiciens de CMS peuvent en déduire l'existence en étudiant les pluies de particules laissées après les collisions proton-proton. (T. McCauley, L. Taylor / CERN) 
Galerie de photos
Contenu connexe
- Art et science se rencontrent à la découverte du boson de Higgs
Une histoire célèbre dans les annales de la physique raconte l'histoire d'Albert Einstein, âgé de 5 ans, malade au lit, qui a reçu une boussole du jouet de son père. Le garçon était à la fois déconcerté et hypnotisé par les forces invisibles au travail, redirigeant l'aiguille du compas vers le nord chaque fois que sa position de repos était perturbée. Einstein dira plus tard que cette expérience l'a convaincu qu'il existait un ordre caché dans la nature et l'a poussé à passer sa vie à essayer de le révéler.
Bien que l'histoire remonte à plus d'un siècle, l'énigme que le jeune Einstein a rencontrée résonne avec un thème clé de la physique contemporaine, un thème essentiel pour la plus importante réalisation expérimentale dans le domaine des 50 dernières années: la découverte, il y a un an, en juillet, du boson de Higgs.
Laisse-moi expliquer.
La science en général et la physique en particulier recherchent des modèles. Étirez un ressort deux fois plus loin et ressentez deux fois la résistance. Un motif. Augmentez le volume occupé par un objet tout en gardant sa masse fixe, et plus il flotte dans l’eau. Un motif. En observant attentivement les modèles, les chercheurs découvrent des lois physiques qui peuvent être exprimées dans le langage des équations mathématiques.
Un motif clair est également évident dans le cas d'une boussole: déplacez-la et l'aiguille pointe à nouveau vers le nord. Je peux imaginer un jeune Einstein pensant qu'il doit exister une loi générale stipulant que les aiguilles métalliques suspendues sont repoussées vers le nord. Mais une telle loi n'existe pas. Lorsqu'il y a un champ magnétique dans une région, certains objets métalliques subissent une force qui les aligne dans la direction du champ, quelle que soit cette direction. Et le champ magnétique de la Terre se trouve au nord.
L'exemple est simple mais la leçon est profonde. Les schémas de la nature reflètent parfois deux caractéristiques imbriquées: les lois physiques fondamentales et les influences environnementales. C'est la version de la nature entre nature et culture. Dans le cas d'une boussole, démêler les deux n'est pas difficile. En le manipulant avec un aimant, vous concluez facilement que l'orientation de l'aimant détermine la direction de l'aiguille. Mais il peut y avoir d'autres situations où les influences environnementales sont si omniprésentes, et au-delà de notre capacité de manipulation, il serait beaucoup plus difficile de reconnaître leur influence.
Les physiciens racontent une parabole sur des poissons qui étudient les lois de la physique, mais qui sont tellement habitués à leur monde aquatique qu'ils ne tiennent pas compte de son influence. Les poissons luttent puissamment pour expliquer le léger balancement des plantes ainsi que leur propre locomotion. Les lois qu'ils trouvent finalement sont complexes et difficiles à manier. Ensuite, un poisson brillant a une percée. Peut-être que la complexité reflète de simples lois fondamentales qui agissent dans un environnement complexe, rempli d’un fluide visqueux, incompressible et omniprésent: l’océan. Au début, le poisson perspicace est ignoré, même ridiculisé. Mais lentement, les autres réalisent aussi que leur environnement, malgré sa familiarité, a un impact significatif sur tout ce qu'ils observent.
La parabole est-elle plus proche de chez nous que nous l’aurions pensé? Y a-t-il d'autres caractéristiques de l'environnement, subtiles mais omniprésentes, que nous n'avons jusqu'à présent pas réussi à intégrer correctement à notre compréhension? La découverte de la particule de Higgs par le grand collisionneur de hadrons à Genève a convaincu les physiciens que la réponse est un oui retentissant.
Il y a près d'un demi-siècle, Peter Higgs et une poignée d'autres physiciens tentaient de comprendre l'origine d'une caractéristique physique fondamentale: la masse. Vous pouvez considérer la masse comme le poids d'un objet ou, un peu plus précisément, par la résistance qu'il offre à la modification de son mouvement. Poussez sur un train de marchandises (ou une plume) pour augmenter sa vitesse, et la résistance que vous ressentez reflète sa masse. Au niveau microscopique, la masse du train de marchandises provient de ses molécules et atomes constitutifs, eux-mêmes construits à partir de particules fondamentales, d'électrons et de quarks. Mais d'où viennent les masses de ces particules fondamentales et d'autres?
Lorsque, dans les années 1960, les physiciens ont modélisé le comportement de ces particules à l'aide d'équations issues de la physique quantique, ils ont rencontré un casse-tête. S'ils imaginaient que les particules étaient toutes dépourvues de masse, alors chaque terme des équations s'inscrirait dans un motif parfaitement symétrique, comme les pointes d'un flocon de neige parfait. Et cette symétrie n'était pas seulement mathématiquement élégante. Cela expliquait les tendances évidentes dans les données expérimentales. Mais - et voici le puzzle - les physiciens savaient que les particules avaient effectivement une masse, et quand ils ont modifié les équations pour tenir compte de ce fait, l'harmonie mathématique a été gâchée. Les équations sont devenues complexes et lourdes et, pire encore, incohérentes.
Que faire? Voici l'idée avancée par Higgs. Ne jetez pas les masses de particules dans la gorge des belles équations. Au lieu de cela, conservez les équations primitives et symétriques, mais considérez qu'elles fonctionnent dans un environnement particulier. Imaginez que tout l’espace soit uniformément rempli d’une substance invisible, appelée désormais champ de Higgs, qui exerce une force de traînée sur les particules lorsqu’elles accélèrent. Appuyez sur une particule fondamentale pour augmenter sa vitesse et, selon Higgs, vous sentiriez cette force de traînée comme une résistance. À juste titre, vous interpréteriez la résistance comme la masse de la particule. Pensez à une balle de ping-pong immergée dans l’eau. Lorsque vous appuyez sur la balle de ping-pong, elle se sentira beaucoup plus massive qu’elle ne l’est hors de l’eau. Son interaction avec l'environnement aqueux a pour effet de le doter de masse. Donc, avec des particules immergées dans le champ de Higgs.
En 1964, Higgs soumit un article à une importante revue de physique dans laquelle il formula cette idée de manière mathématique. Le papier a été rejeté. Non pas parce que cela contenait une erreur technique, mais parce que le principe de base de quelque chose d'invisible qui imprègne l'espace, interagissant avec les particules pour fournir leur masse, eh bien, tout cela ressemblait à des tas de spéculations excessives. Les rédacteurs en chef de la revue ont estimé qu'il "n'avait aucune pertinence évidente pour la physique".
Mais Higgs a persévéré (et son article révisé a paru plus tard dans un autre journal) et les physiciens qui ont pris le temps d'étudier la proposition se sont peu à peu rendus compte que son idée était un coup de génie, qui leur permettait d'avoir leur gâteau et de le manger aussi. . Dans le schéma de Higgs, les équations fondamentales peuvent conserver leur forme primitive car le travail délicat consistant à fournir les masses des particules est relégué à l'environnement.
Bien que je n'étais pas là pour assister au rejet initial de la proposition de Higgs en 1964 (eh bien, j'étais autour, mais à peine), je peux attester qu'au milieu des années 1980, l'évaluation avait changé. La plupart des spécialistes de la physique avaient pleinement souscrit à l'idée qu'il existait un champ de Higgs imprégnant l'espace. En fait, dans un cours de troisième cycle que j'ai suivi, qui portait sur ce que l'on appelle le modèle standard de la physique des particules (les physiciens du système d'équations quantiques se sont assemblés pour décrire les particules de la matière et les forces dominantes par lesquelles elles s'influencent mutuellement), le professeur a présenté le Higgs terrain avec une telle certitude que pendant longtemps, je ne savais pas qu’il devait encore être établi à titre expérimental. Cela se produit parfois en physique. Les équations mathématiques peuvent parfois raconter une histoire si convaincante, elles peuvent apparemment rayonner la réalité avec une telle force, qu'elles sont enracinées dans la langue vernaculaire des physiciens en activité, avant même que des données les confirment.
Mais ce n’est qu’avec les données qu’un lien avec la réalité peut être créé. Comment pouvons-nous tester le champ de Higgs? C’est là que le Grand collisionneur de hadrons (LHC) entre en jeu. Le LHC, qui traverse des centaines de mètres sous Genève et traverse la frontière française, est un tunnel circulaire de près de 17 km de long qui sert de piste brisant ensemble des particules de matière. Le LHC est entouré d'environ 9 000 aimants supraconducteurs et héberge des hordes de protons qui défilent, circulant dans le tunnel dans les deux sens, accélérant à une vitesse très proche de la vitesse de la lumière. À de telles vitesses, les protons tournent autour du tunnel environ 11 000 fois par seconde et, lorsqu'ils sont dirigés par les aimants, engagent des millions de collisions en un clin d'œil. Les collisions génèrent à leur tour des pulvérisations de particules, que des détecteurs de mammouth capturent et enregistrent.
L'une des principales motivations du LHC, qui coûte environ 10 milliards de dollars et implique des milliers de scientifiques de dizaines de pays, a été de rechercher des preuves pour le champ de Higgs. Les calculs ont montré que si l'idée est bonne, si nous sommes vraiment immergés dans un océan de champs de Higgs, les collisions violentes de particules devraient pouvoir secouer le champ, tout comme deux sous-marins en collision secoueraient l'eau autour d'eux. Et de temps à autre, l'agitation devrait être juste de jeter un coup d'œil sur un point du champ - une minuscule gouttelette de l'océan de Higgs - qui apparaîtrait comme la particule de Higgs tant recherchée.
Les calculs ont également montré que la particule de Higgs serait instable, se désintégrant en d’autres particules en une fraction de seconde. Dans le tourbillon de particules en collision et de nuages flottants de débris particulaires, des scientifiques armés de puissants ordinateurs pourraient rechercher l'empreinte digitale de Higgs, un ensemble de produits de désintégration dictés par les équations.
Tôt le matin du 4 juillet 2012, je me suis réuni avec une vingtaine de fidèles dans une salle de conférence du Aspen Center for Physics pour regarder en direct une conférence de presse dans les installations du Grand collisionneur de hadrons à Genève. Environ six mois plus tôt, deux équipes indépendantes de chercheurs responsables de la collecte et de l'analyse des données du LHC avaient annoncé une forte indication de la découverte de la particule de Higgs. La rumeur qui circule à l’heure actuelle dans la physique est que les équipes disposaient enfin de suffisamment de preuves pour revendiquer de façon définitive. En plus du fait que Peter Higgs lui-même avait été invité à faire le voyage à Genève, il y avait de quoi être motivé pour rester au-dessus de 3 heures du matin pour entendre l'annonce en direct.
Et à mesure que le monde apprenait rapidement, la preuve que la particule de Higgs avait été détectée était suffisamment solide pour franchir le seuil de la découverte. Avec la particule de Higgs maintenant officiellement retrouvée, le public à Genève a éclaté sous les applaudissements, de même que notre petit groupe à Aspen, et sans doute des dizaines de rassemblements similaires dans le monde entier. Peter Higgs essuya une larme.
Avec un an de recul et des données supplémentaires qui n'ont servi qu'à renforcer les arguments des Higgs, voici comment je résumerais les implications les plus importantes de la découverte.
Premièrement, nous savons depuis longtemps qu'il y a des habitants invisibles dans l'espace. Ondes radio et télévision. Le champ magnétique terrestre Champs gravitationnels. Mais aucun de ceux-ci n'est permanent. Aucun n'est immuable. Aucun n'est uniformément présent dans tout l'univers. À cet égard, le domaine de Higgs est fondamentalement différent. Nous pensons que sa valeur est la même sur Terre qu’à proximité de Saturne, dans les nébuleuses d’Orion, dans toute la galaxie d’Andromède et partout ailleurs. Autant que nous puissions en juger, le champ de Higgs est imprimé de manière indélébile dans la structure spatiale.
Deuxièmement, la particule de Higgs représente une nouvelle forme de matière, largement anticipée depuis des décennies mais jamais vue auparavant. Au début du XXe siècle, les physiciens ont compris que les particules, outre leur masse et leur charge électrique, ont une troisième caractéristique déterminante: leur spin. Mais contrairement au sommet d'un enfant, le spin d'une particule est une caractéristique intrinsèque qui ne change pas. cela ne s'accélère pas et ne ralentit pas avec le temps. Les électrons et les quarks ont tous la même valeur de spin, tandis que le spin des photons - particules de lumière - est le double de celui des électrons et des quarks. Les équations décrivant la particule de Higgs ont montré que, contrairement à toute autre espèce de particule fondamentale, elle ne devrait pas tourner du tout. Les données du grand collisionneur de hadrons l'ont maintenant confirmé.
Établir l'existence d'une nouvelle forme de matière est une réalisation rare, mais le résultat a une résonance dans un autre domaine: la cosmologie, l'étude scientifique de la façon dont l'univers entier a commencé et s'est développé sous la forme que nous observons maintenant. Pendant de nombreuses années, les cosmologistes étudiant la théorie du Big Bang ont été bloqués. Ils avaient préparé une description robuste de la façon dont l'univers avait évolué d'une fraction de seconde après le début, mais ils étaient incapables de donner une idée de ce qui avait conduit l'espace à commencer à se développer. Quelle force aurait pu exercer une poussée extérieure aussi puissante? Malgré tout son succès, la théorie du Big Bang a laissé de côté le bang.
Dans les années 1980, une solution possible a été découverte, celle qui sonne à haute voix. Si une région de l’espace est uniformément imprégnée d’un champ dont les constituants sont dépourvus de spin, la théorie de la gravité d’Einstein (la théorie de la relativité générale) révèle qu’une force répulsive puissante peut être générée - une détonation puissante. Les calculs ont montré qu'il était difficile de concrétiser cette idée avec le champ de Higgs lui-même; le double devoir de fournir des masses de particules et d'alimenter la détonation constitue un fardeau considérable. Mais des scientifiques perspicaces ont réalisé qu’en posant un second champ de type «Higgs» (possédant le même effet de fuite, mais une masse et des interactions différentes), ils pourraient se répartir la charge - un champ pour la masse et l’autre pour la poussée répulsive - et offrir une explication convaincante de la détonation. Pour cette raison, depuis plus de 30 ans, les physiciens théoriciens explorent avec vigueur les théories cosmologiques dans lesquelles de tels champs de type Higgs jouent un rôle essentiel. Des milliers d'articles de revues ont été écrits pour développer ces idées, et des milliards de dollars ont été dépensés pour des observations dans l'espace lointain cherchant - et trouvant - des preuves indirectes du fait que ces théories décrivent avec précision notre univers. La confirmation du LHC selon laquelle au moins un tel champ existe réellement place donc une génération de théories cosmologiques sur des bases beaucoup plus solides.
Enfin, et peut-être le plus important, la découverte de la particule de Higgs est un étonnant triomphe du pouvoir des mathématiques de révéler le fonctionnement de l'univers. C'est une histoire qui a été récapitulée à maintes reprises dans la physique, mais chaque nouvel exemple fait la même chose. La possibilité de trous noirs a émergé des analyses mathématiques du physicien allemand Karl Schwarzchild; les observations ultérieures ont prouvé que les trous noirs sont réels. La cosmologie du Big Bang est issue des analyses mathématiques d'Alexander Friedmann et de Georges Lemaître; les observations ultérieures ont également prouvé cette idée. Le concept d'anti-matière est apparu pour la première fois à partir des analyses mathématiques du physicien quantique Paul Dirac; les expériences ultérieures ont montré que cette idée est également valable. Ces exemples donnent une idée de ce que le grand physicien mathématique Eugene Wigner voulait dire quand il parlait de «l’efficacité déraisonnable des mathématiques pour décrire l’univers physique». Le champ de Higgs a émergé d’études mathématiques cherchant un mécanisme permettant de donner de la masse aux particules. Et une fois de plus, les calculs sont brillants.
En tant que physicien théoricien, je suis l'un des nombreux à rechercher ce que Einstein a appelé la «théorie unifiée»: les liens profondément cachés entre toutes les forces de la nature et la matière dont rêvait Einstein, longtemps après avoir été accrochés à la physique par le mystérieux fonctionnement de la boussole. La découverte des Higgs est particulièrement gratifiante. Notre travail est basé sur les mathématiques et n'a jusqu'à présent pas été mis en contact avec des données expérimentales. Nous attendons avec impatience 2015 quand un LHC mis à niveau et encore plus puissant sera rallumé, car il est fort probable que les nouvelles données montrent que nos théories vont dans la bonne direction. Les principaux jalons seraient la découverte d'une classe de particules inédites (appelées «particules supersymétriques») que nos équations prédisent, ou d'indices de la possibilité sauvage de dimensions spatiales au-delà des trois que nous connaissons tous. Plus excitant encore serait la découverte de quelque chose de complètement inattendu, nous renvoyant tous à nos tableaux noirs.
Beaucoup d'entre nous essayons de gravir ces montagnes mathématiques depuis 30 ans, voire plus longtemps. Nous avons parfois senti que la théorie unifiée était juste au-dessus de nos doigts, alors que d'autres fois, nous étions à tâtons dans le noir. C’est un formidable élan pour notre génération d’être témoin de la confirmation de la loi de Higgs, de témoigner de connaissances mathématiques vieilles de quatre décennies qui se concrétisent sous forme de sauts et de craquements dans les détecteurs LHC. Cela nous rappelle de prendre à cœur les paroles du lauréat du prix Nobel Steven Weinberg: «Notre erreur n'est pas de prendre nos théories trop au sérieux, mais de ne pas les prendre suffisamment au sérieux. Il est toujours difficile de réaliser que les nombres et les équations avec lesquels nous jouons à nos bureaux ont quelque chose à voir avec le monde réel. »Parfois, ces nombres et ces équations ont une capacité étrange, presque inquiétante, d’éclairer des recoins par ailleurs sombres de la réalité. Lorsqu'ils le font, nous nous rapprochons d'autant plus de notre place dans le cosmos.
